Area
The area of a flat, or
plane figure is the number
of unit squares that can be contained within it. The unit square is usually some
standard unit, like a square meter, a square foot, or a square inch.
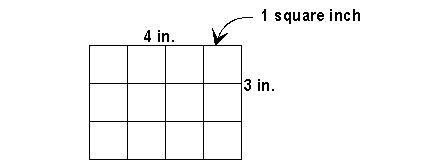
So, if you
are trying to find the area of a sheet of paper that is 9 inches by 11 inches, and
the unit square you want is the square inch, then there are 9 X 11 = 99
square inches in that sheet of paper. In this 4 inch by 3 inch rectangle,
each little square is a square inch. Count the little
one-inch squares and find the total area. Is it the same as multiplying the
width of the rectangle by the height?
Here are the formulas for the area of some common plane figures:
| Circle
| 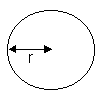 |
A =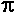 R2 R2 | Click here to see a proof of why
this is the area of a circle. |
| Triangle |
 |
A = B H / 2 | where B is the base and H is the height |
| Trapezoid |
 |
A = (B1 + B2) H / 2 |
Where B1 is the first base
and B2 is the second base and H is the height. (B1 and B2 must be parallel) |
|
 |
A = 3 B H | where B is the length of one side and
H is the distance from the middle
of a side to the center of the hexagon (the apothem) |
Any N-sided
regular polygon |
 |
A = N B H / 2 |
where N is the number of sides.
Think about it. This is just N little triangles whose bases are B and whose heights are H and whose apexes all meet at the center (like cutting a pie), so we have N triangles, each of whose area is (BH/2) |
The area of any regular polygon can be determined by its side length by the following formula:
A = s2 n
4 Pn
where:
s = the side length
n = the number of sides
Pn is a parameter from this table:
|
n
|
Pn
|
3
(an equilateral triangle)
|
1.73205
|
| 4
|
1
|
| 5
|
0.72654
|
| 6
|
0.57735
|
| 7
|
0.48157
|
| 8
|
0.55785
|
| 9
|
0.36397
|
| 10
|
0.32492
|
| 11
|
0.29363
|
| 12
|
0.26795
|
Note: the parameter Pn is a parameter
involving trigonometry which is beyond
the scope of this program.
|
|