
Apothem
The apothem of a regular polygon is a line from the center of the polygon to the midpoint of one of its sides.
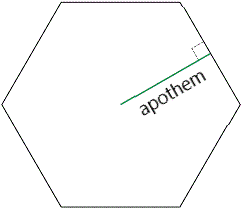
If you know the length of a regular polygon's apothem, you can compute it's area by this formula:
A = N (P L / 2)
| |
Where:
N is the number of sides of the regular polygon,
L is the length of one side and
P is the length of the apothem.
|
Think about it. If you cut up the polygon into
little triangles, each with a base L and a height
P, then this is just the sum of the areas
of all those little triangles.
Each little triangle has area (P L) / 2
and there are N of them,
so the area of the polygon is N (P L) / 2
|
===>
|

P
L
|
If you know your algebra, you can see that if you know the area, A, of the regular polygon, you can get the length of the apothem (P) by this formula: (the above formula turned around!)
P = (2 A) / (N L)
|



