
Rounding
For many problems numbers don't need to be exact. For example, pi (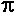 ) has an infinite number of digits but we usually round it off to 3.14. For many problems, this is good enough. Here are the rules for rounding numbers: ) has an infinite number of digits but we usually round it off to 3.14. For many problems, this is good enough. Here are the rules for rounding numbers:
- Decide which is the last digit to keep (the "keep" digit)
For our example of the rounding of 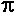 , the "keep" digit is the 4 , the "keep" digit is the 4
- Leave it the same if the next digit is less than 5 (this is called rounding down)
- Increase it by 1 if the next digit is 5 or more (this is called rounding up)
- Put in zeroes for rounded off numbers past the "keep" digit if the keep digit is the 10s digit or higher.
In the case of pi (3.14) the next digit after the 4 is 1 (3.141) so we leave the 4 the same. This is rounding to the nearest hundredth because the 4 is the hundredths digit.
Here is an example, the number 4827.1836:
Round to . . .
| "keep"
digit
↓ | rounded
number |
Comments
|
| Nearest thousandth | 4827.1836 | 4827.184 | 3 changed to 4 because 3 was followed by 6 |
| Nearest hundredth | 4827.1836 | 4827.18 |
| Nearest tenth | 4827.1836 | 4827.2 |
| Nearest whole number | 4827.1836 | 4827 |
| Nearest ten | 4827.1836 | 4830 | added a zero |
| Nearest hundred | 4827.1836 | 4800 | added 2 zeroes |
| Nearest thousand | 4827.1836 | 5000 | 4 changed to 5 because 4 was followed by 8 |
Now here are some problems for you:
- Round 56 to the nearest ten = ______
- Round 4.159 to the nearest tenth = _____
- Round 36.66666 to the nearest hundredth = _____
- Round 22.7828 to the nearest whole number = ______
|

 ) has an infinite number of digits but we usually round it off to 3.14. For many problems, this is good enough. Here are the rules for rounding numbers:
) has an infinite number of digits but we usually round it off to 3.14. For many problems, this is good enough. Here are the rules for rounding numbers:

 ) has an infinite number of digits but we usually round it off to 3.14. For many problems, this is good enough. Here are the rules for rounding numbers:
) has an infinite number of digits but we usually round it off to 3.14. For many problems, this is good enough. Here are the rules for rounding numbers: