
Polygon Interior Angles
Here's how that's computed: We'll use a pentagon as an example. Start with a pentagon and locate its center: 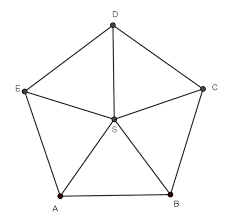 360o/5 = 72o That makes the sum of the other 2 angles of each triangle 180o - 72o = 108o. Each of the other angles of the triangle are 108/2 = 54o Looking at the image you can see that 2 of these angles makes a pentagon interior angle, so the interior angles of a pentagon are 108o each. 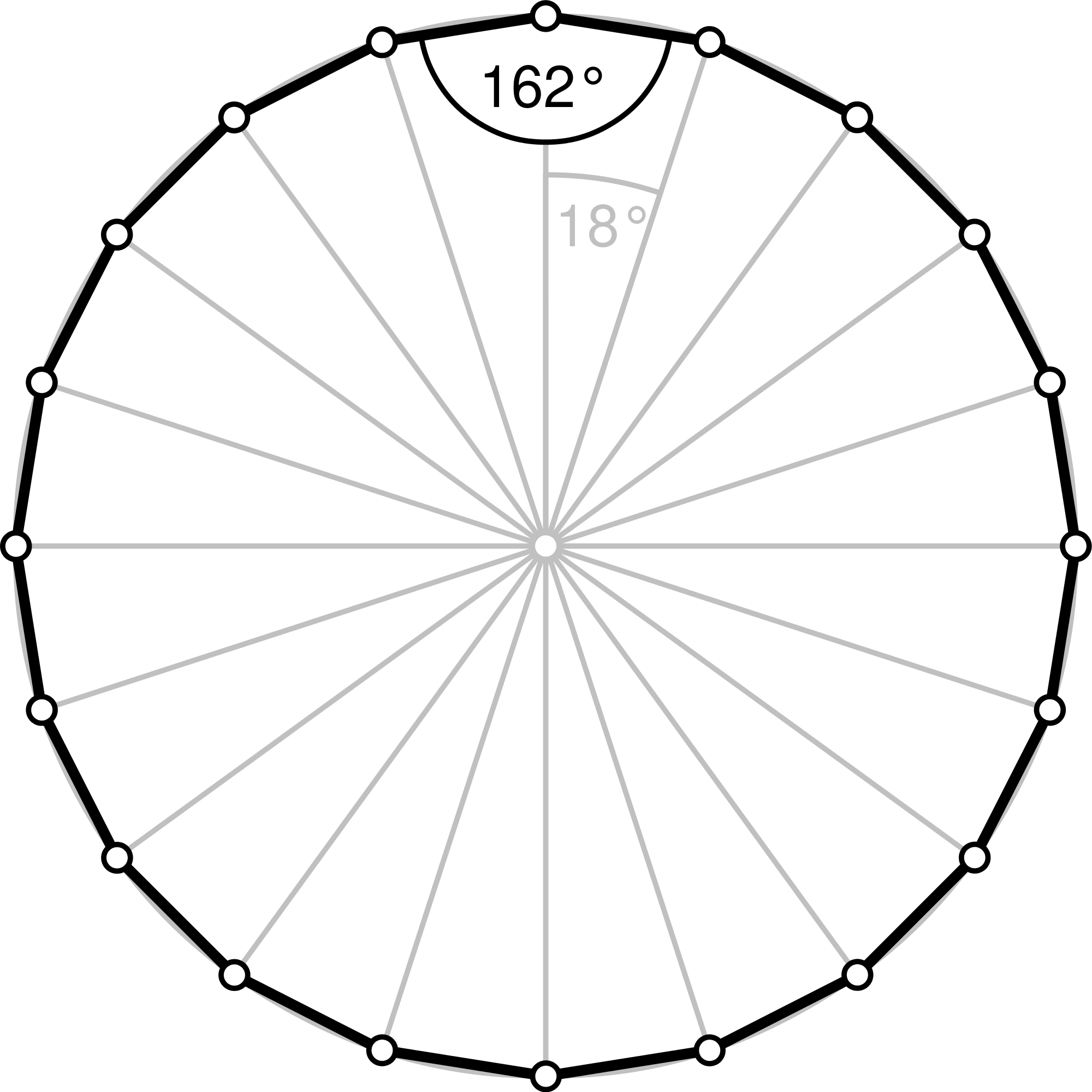 Let's try this on a larger polygon, one with 20 sides!
Let's try this on a larger polygon, one with 20 sides!So, all the triangles vertices meet at the center and there are 20 of them, so each triangle vertex angle = 360o/20o = 18o That makes the sum of the other 2 angles 180o - 18o = 162o which is the size of the interior angle of a 20-sided figure which, by the way, is an icosagon. |
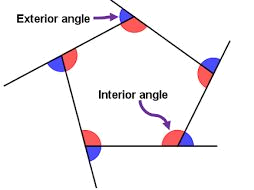 The interior angles of a
The interior angles of a